Importance Driven Coverage
Importance Driven Coverage of Deep Learning Systems
Author Information
Simos Gerasimou - University of York
Hasan Ferit Eniser - MPI-SWS
Alper Sen - Bogazici University
Alper Cakan - Bogazici University
Source Code
https://github.com/DeepImportance/deepimportance_code_release
Abstract
Deep Learning (DL) systems are key enablers for engineering intelligent applications due to their ability to solve complex tasks such as image recognition and machine translation. Nevertheless, using DL systems in safety- and security-critical applications requires to provide testing evidence for their dependable operation. Recent research in this direction focuses on adapting testing criteria from traditional software engineering as a means of increasing confidence for their correct behaviour. However, they are inadequate in capturing the intrinsic properties exhibited by these systems. We bridge this gap by introducing DeepImportance, a systematic testing methodology accompanied by an Importance-Driven (IDC) test adequacy criterion for DL systems. Applying IDC enables to establish a layer-wise functional understanding of the importance of DL system components and use this information to guide the generation of semantically-diverse test sets. Our empirical evaluation on several DL systems, across multiple DL datasets and with state-of-the-art adversarial generation techniques demonstrates the usefulness and effectiveness of DeepImportance and its ability to guide the engineering of more robust DL systems.
We have also made available the soundness proof for the IDC introduced in the paper. Click here.
Overview
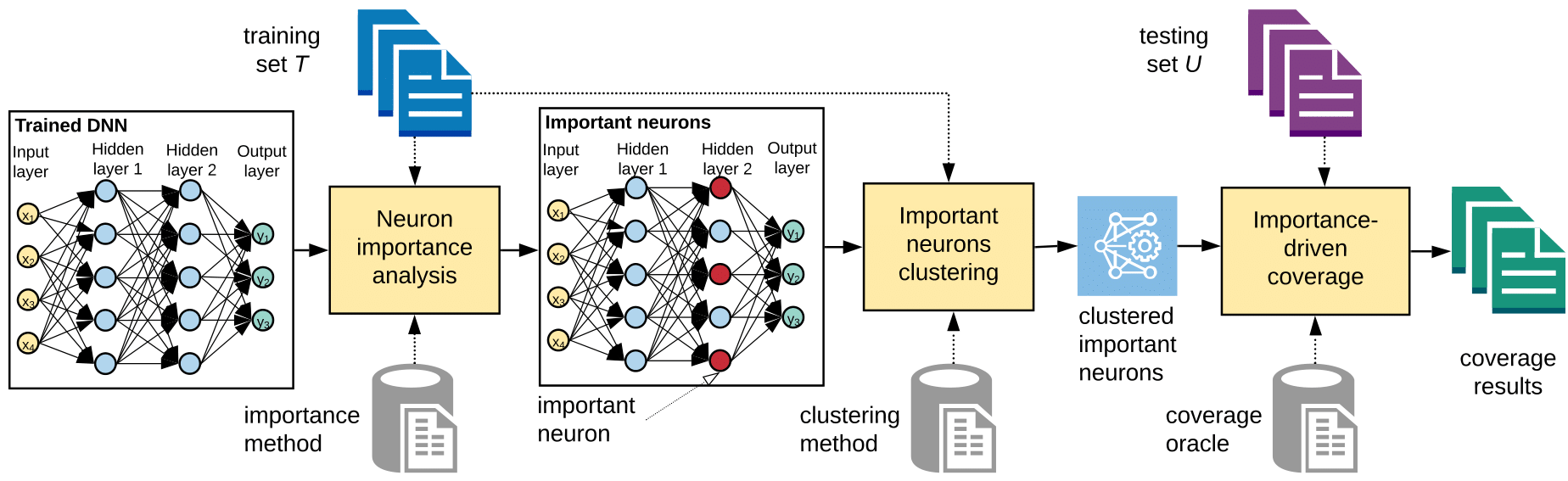
Using a pre-trained DL system, DeepImportance analyses the training set T to establish a fundamental understanding of the overall contribution made by internal neurons of the DL system. This enables to identify the most important neurons that are core contributors to the decision-making process. Then, DeepImportance carries out a quantisation step which produces an automatically-determined finite set of clusters of neuron activation values that characterises, to a sufficient level, how the behaviour of the most important neurons changes with respect to inputs from the training set. Finally, DeepImportance uses the produced clusters of the most important neurons to assess the coverage adequacy of the test set. Informally, the Importance-Driven test adequacy criterion of DeepImportance is satisfied when all combinations of important neurons clusters are exercised.
Neuron Importance Analysis
The purpose of importance analysis is to identify neurons within a DL system that are key contributors to decision-making. We capitalise on this unique characteristic of neurons within a trained DL system to establish the importance of each neuron. To achieve this, we compute a decomposition of the decision f(x) made by the system for input x ∈ X and use layer-wise relevance propagation [1] to traverse the network graph and redistribute the decision value in a layer-wise manner proportional to the contribution made by each neuron within the layer. When the relevance propagation is iterated until the input layer, it provides relevance score for each individual raw feature (e.g. pixel, characters etc). Below there are two examples of relevance propagation analysis iterated until the input layer.
The red colored words in the text below represent their high relevance to the classification decision (i.e. cars) of the DNN that is trained for text classification.
The red colored pixels in the image below represent their high relevance to the classification decision (i.e. 6) of the DNN that is trained for handwritten image classification.

Importance Neuron Clustering
DeepImportance employs k-means to cluster the vector of activation values from the training set for each important neuron and determine sets of values that can be grouped together.
The purpose of clustering is threefold.
-
Compared to [2] which partitions the value range of neuron activation values into k buckets of equal width solely based on a randomly selected number of buckets, the clusters generated by our approach correspond to semantically different features of each neuron.
-
Since the range of neuron activation values φ(x,n) could in principle be the entire set of real numbers, the cyclomatic complexity for analysing the DL system is very large. Clustering enables to reduce dimensionality and computational costof testing DL system.
-
The identification of clusters for those important neurons informs the allocation of testing resources to ensure that the regions of those neurons are tested sufficiently, thus increasing our confidence for the robust DL system behaviour.
Importance-Driven Coverage (IDC)
Since important neurons are core contributors in decision-making, it is significant to establish that inputs triggering combinations of activation value clusters of those neurons have been covered adequately. The vector of important neurons cluster combinations (INCC) is given by
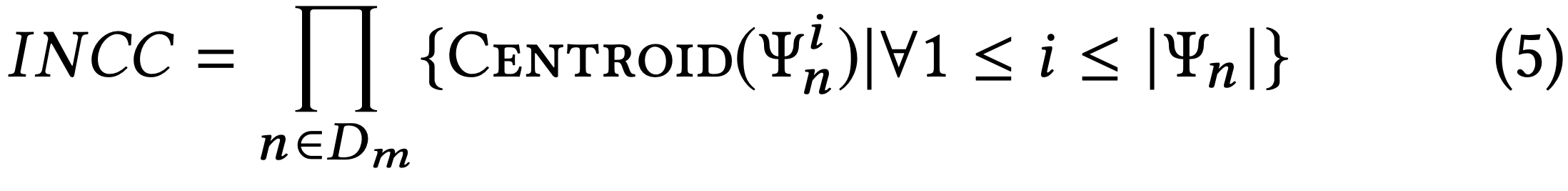
where the function Centroid(Ψ_i^n)measures the “centre of mass”of the i-th cluster for the n-th important neuron. We define Importance-Driven Coverage (IDC) to be the ratio of INCC covered by all y ∈ Y over the size of the INCC set. Formally:
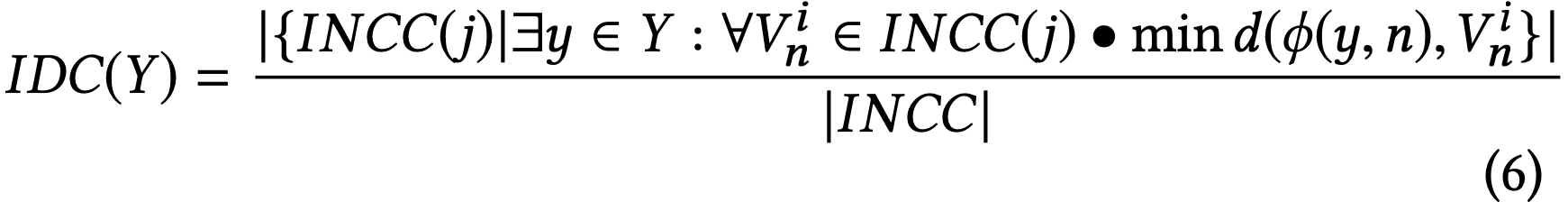
IDC soundness proof can be found here .
Achieving a high IDC score entails a systematically diverse input set that exercises many combinations of important neurons clusters. Consequently, the more confidence we should have in the DL system’s operation. Another important characteristic of IDC is the layer-wise estimation of coverage.
Implementation
We provide the required information and the source code to reproduce the results presented in the paper. DeepImportance implementation can be found in https://github.com/YYY/DeepImportance. The implementation makes use of Keras(v2.2.2) and Tensorflow(v1.10.1) libraries. Hyperparameter selection in our evaluation is presented below.
Hyperparameters Chosen In Evaluation
CW:
batch_size=1,
confidence=0,
learning_rate=5e-3,
binary_search_steps=5,
max_iterations=1000,
abort_early=True,
initial_const=1e-2,
clip_min=0,
clip_max=1
FGSM:
eps=0.3,
ord=np.inf,
y=None,
y_target=None,
clip_min=None,
clip_max=None,
clip_grad=False,
sanity_checks=True,
BIM:
eps=0.3,
eps_iter=0.05,
nb_iter=10,
y=None,
ord=np.inf,
clip_min=None,
clip_max=None,
y_target=None,
rand_init=None,
rand_init_eps=None,
clip_grad=False
JSMA:
theta=1,
gamma=1,
clip_min=0,
clip_max=1,
y_target=None,
symbolic_impl=True
Training Parameters for LeNet Models:
loss = 'categorical_crossentropy'
optimizer = 'adadelta' --> (learning_rate=1.0, rho=0.95)
metrics = ['accuracy']
batch_size = 256,
epochs = 10
Training Parameters for CIFAR Model:
loss = 'categorical_crossentropy'
optimizer = 'RMSprop' --> (learning_rate=0.0001, decay=1e-6)
metrics = ['accuracy']
batch_size = 32,
epochs = 40
Training Parameters for DAVE Model:
loss = 'mse'
optimizer = 'adadelta' --> (learning_rate=1.0, rho=0.95)
batch_size = 256,
epochs = 10
Evaluation
Experimental Setup
Datasets and DL Systems
Table below shows the datasets and DL systems used in our experimental evaluation.
| Dataset | DL System | #Params | Performance |
|---|---|---|---|
| MNIST | LeNet-1 | 7206 | 98.33% |
| MNIST | LeNet-4 | 69262 | 98.59% |
| MNIST | LeNet-5 | 107786 | 98.96% |
| CIFAR-10 | A 20 layer ConvNet | 952234 | 77.68% |
| Self-driving data | Dave-2 | 2116983 | 0.096 (MSE) |
Coverage Criteria Configurations
We facilitate a thorough and unbiased evaluation of DeepImportance by comparing it against state-of-the-art coverage criteria for DL systems. To this end, we used DeepXplore’s neuron coverage (NC); DeepGauge’s k-multisection neuron coverage (KMNC), neuron boundary coverage (NBC), strong neuron activation coverage (SNAC) and top-k neuron coverage (TKNC); and Surprise’s Adequacy distance-based (DSC) and likelihood-based surprise coverage (LSC). For each criterion, we use the hyper-parameters recommended in its original research.
Synthetic Inputs and Adversarial Examples
We use both syn thetic inputs and adversarial examples to evaluate DeepImpor- tance. Synthetic inputs are obtained by applying small perturbations on the original inputs through Gaussian-like injected white noise. We employ four widely studied adversarial attack strategies to evaluate DeepImportance Fast Gradient Sign Method (FGSM), Basic Iterative Method (BIM), Jacobian-based Saliency Map Attack (JSMA) , and Carlini&Wagner (C&W). Our implementation of these strategies is based on Cleverhans library.
Research Questions
Our experimental evaluation answers the research questions below.
Importance
RQ1 (Importance): Can neuron-importance analysis identify the most important neurons?
We used this research question to establish if the importance-based algorithm underpinning DeepImportance for the identification of important neurons comfortably outperforms a strategy that selects such neurons randomly.
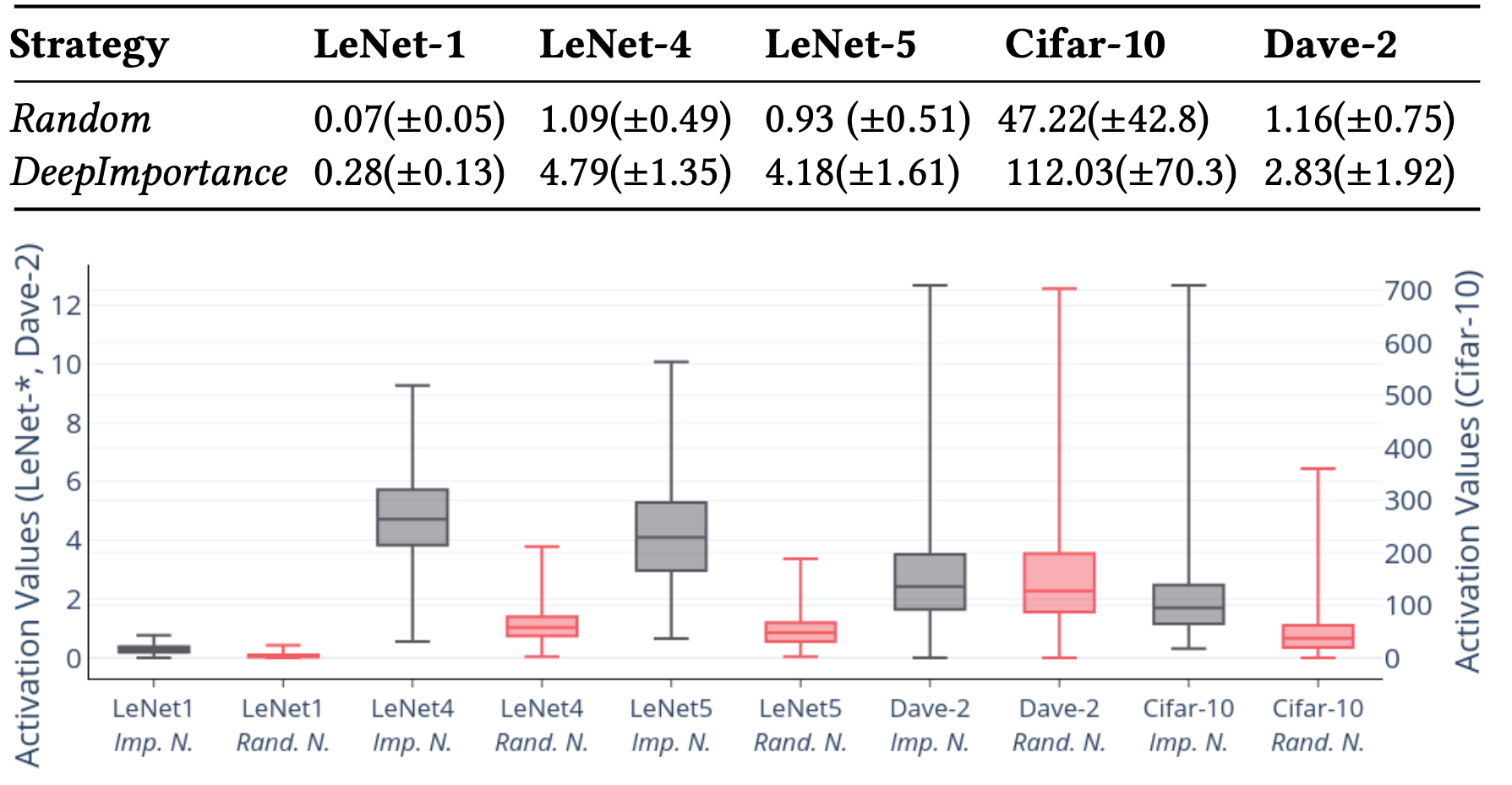
Outcome: We conclude that DeepImportance can detect the most important neurons of a DL system and those neurons are more sensitive to changes in relevant pixels of a given input.
Diversity
RQ2 (Diversity): Can DeepImportance inform the selection of a diverse test set?
We investigate whether software engineers an employ the IDC to generate a diverse test set that comprises semantically different test inputs.
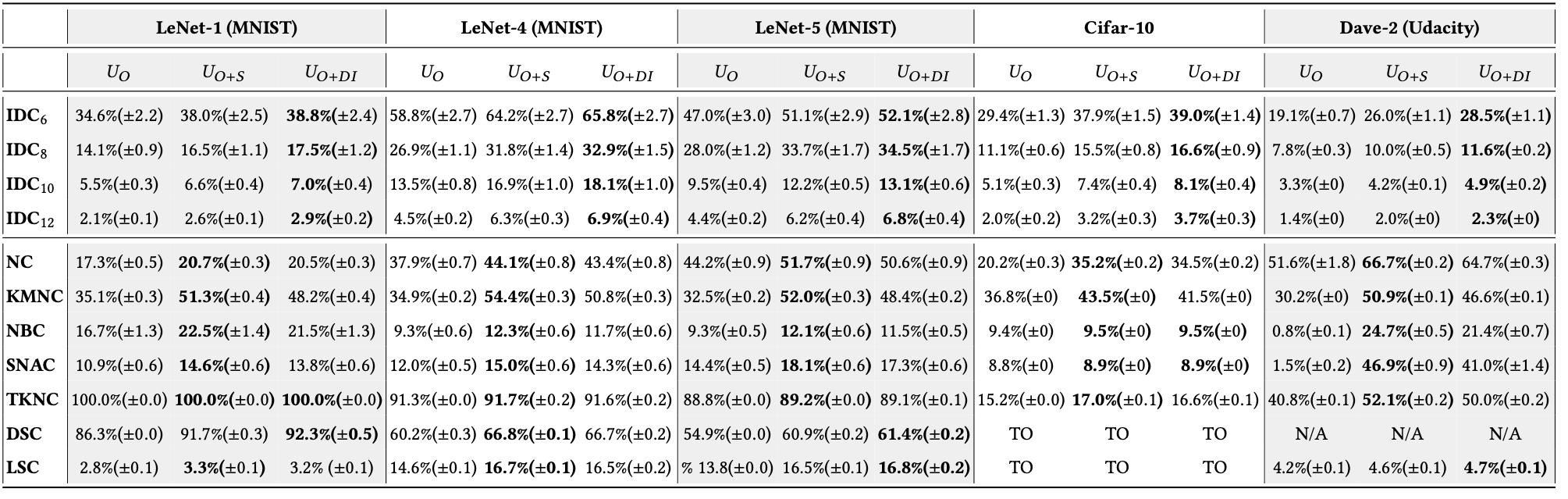
Outcome: We conclude that DeepImportance with its IDC coverage criterion can support software engineers to create a diverse test set that comprises semantically different test inputs.
Effectiveness and Correlation
RQ3 (Effectiveness): How effective is DeepImportance in identifying misbehaviours in DL systems?
With this research question, we examine the effectiveness of DeepImportance to detect adversarial inputs carefully crafted by state-of-the-art adversarial generation techniques.
RQ4 (Correlation): How is DeepImportance correlated with existing coverage criteria for DL systems?
We analyse the relationship in behaviour between DeepImportance and state-of-the-art coverage criteria for DL systems.
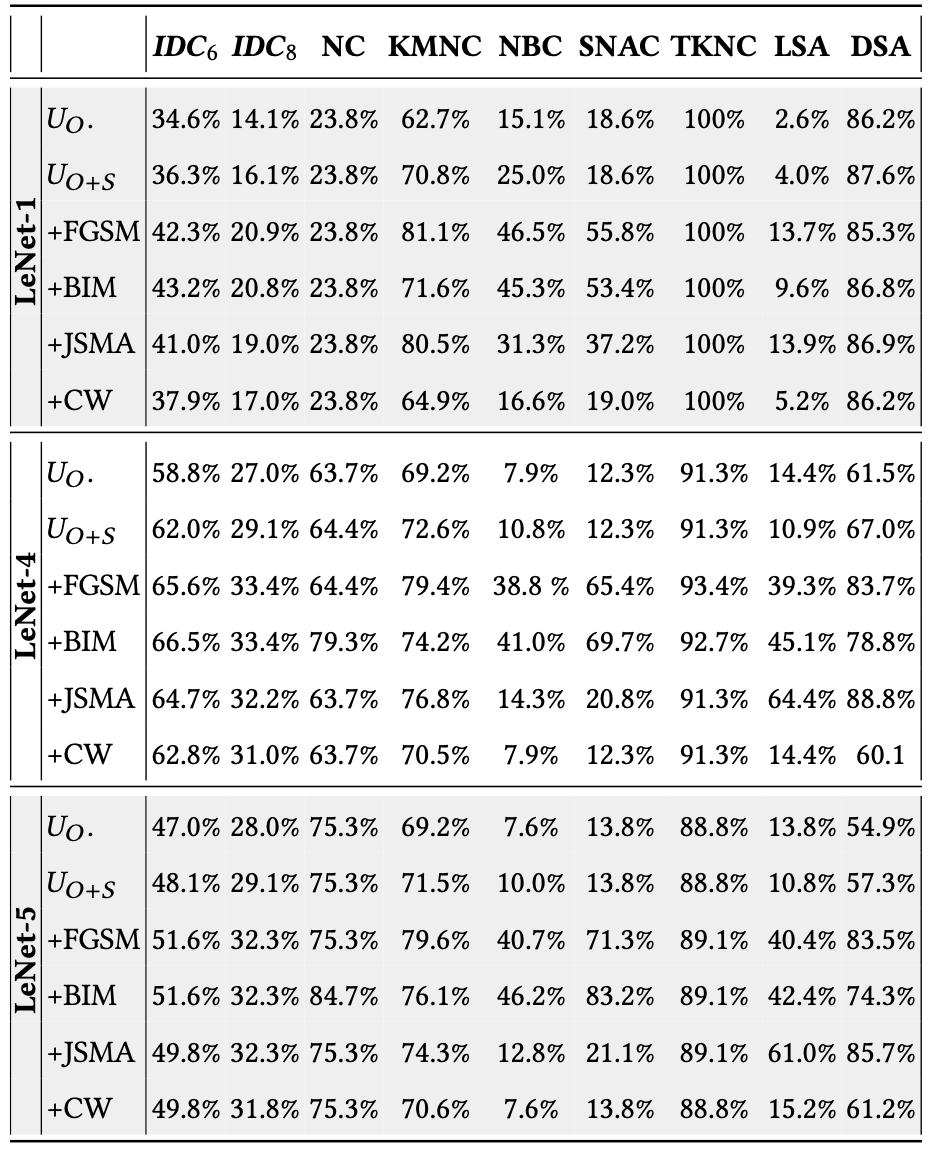
Outcome (Effectiveness): We conclude that IDC is sensitive to adversarial inputs and is effective in detecting misbehaviours in test sets with inputs semantically different than those encountered before.
Outcome (Correlation): In general, we conclude that IDC shows a similar behaviour to state-of-the-art coverage criteria for DL systems; hence, there is a positive correlation between them
Layer Sensitivity
RQ5 (Layer Sensitivity): How is the behaviour of DeepImportance affected by the selection of specific neuron layers?
Given the layer-wise capability of DeepImportance, we investigate whether performing the analysis on shallow or deeper layers has any impact on IDC.

Outcome: Overall, the chosen target layer affects the result of IDC. Since the penultimate layer is responsible to understand semantically-important high-level features, we argue it is a suitable choice to assess the adequacy of a test set using IDC.
Robustness Not included in the paper.
RQ6 (Robustness) Can DeepImportance be used to enhance a DNN against inputs whose important features are missing?
IDC requires semantically diverse inputs to be satisfied. We examine if a DNN can be enhanced by augmenting its training set with the inputs that are increasing IDC.
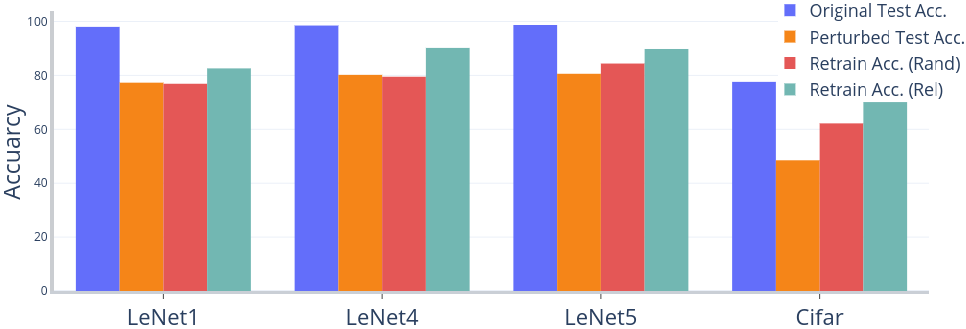
Outcome: We observe that augmenting the training set with inputs that are produced to increase IDC can be used to increase robustness of DNNs against perturbed inputs. On the other hand, inputs generated by random perturbations can not help.